|
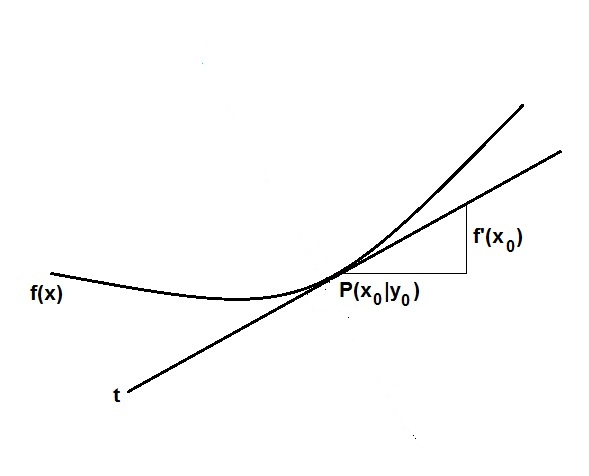
Abbildung:
Funktion f(x), Stelle x0 -> Punkt P(x0|f(x0)) = P(x0|y0) -> Ableitungen f'(x0), f''(x0) usw.
-> Tangente, Taylorpolynome an Funktion im Punkt: T0: y = f(x0),
T1 = t: y = f'(x0)(x-x0) + f(x0), T2: y = f''(x0)(x-x0)2/2 + f'(x0)(x-x0) + f(x0) usw.
Näherungen für die Ableitungen:
f'(x0) = (f(x0+h)-f(x0-h))/2/h, f''(x0) = (f(x0+h)-2f(x0)+f(x0-h))/h2,
f'''(x0) = (f(x0+2h)-2f(x0+h)+2f(x0-h)-f(x0-2h))/2/h3,
f(4)(x0) = (f(x0+2h)-4f(x0+h)+6f(x0)-4f(x0-h)+f(x0-2h))/h4 (hier: h=0.001; Rundungsfehler beachten!).
Funktionseingabe (gemäß JavaScript): Variable x, Klammern (), Addition +, Subtraktion -, Multiplikation *, Division /,
Betrag |x| = Math.abs(x), Potenzfunktion xn = Math.pow(x,n), Wurzelfunktion √x = Math.sqrt(x), Exponentialfunktion ex = Math.exp(x), natürlicher Logarithmus ln(x) = Math.log(x),
trigonometrische Funktionen sin(x) = Math.sin(x), cos(x) = Math.cos(x), tan(x) = Math.tan(x), trigonometrische Umkehrfunktionen arcsin(x) = Math.asin(x), arccos(x) = Math.acos(x), arctan(x) = Math.atan(x).
Eingabe von Funktion, x-Wert (Dezimalzahlen mit Punkt statt Komma, Bruch in der Form Zähler/Nenner): |
 |
