Mathematik
> Bestimmtes Integral

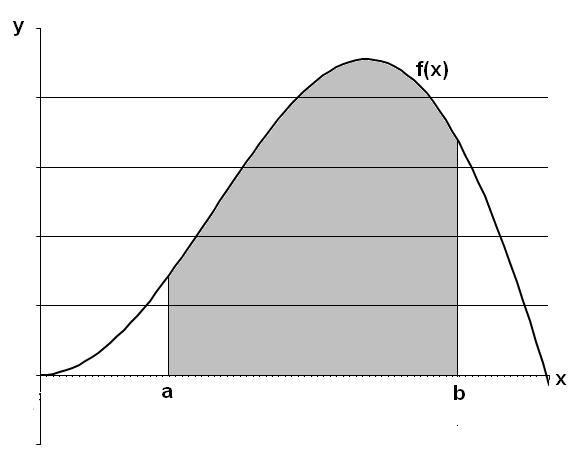
Bestimmtes Integral einer integrierbaren Funktion f(x) auf einem Intervall [a; b] als Summe von von durch quadratische Funktionen begrenzten Flächen über Teilintervallen A_Si = Σ_i=1ⁿ h_n[f(x_2i-2)+4f(x_2i-1)+f(x_2i)]/3 (h_n = (b-a)/2n = Teilintervallbreite, f(x_i) = Funktionswerte der Teilintervallränder und -mitten, 2n = Teilintervallanzahl) -> A = _a∫^b f(x) dx als Flächensaldo bzw. Fläche.

Funktionseingabe (gemäß JavaScript): Variable x, Klammern (), Addition +, Subtraktion -, Multiplikation *, Division /, Betrag |x| = Math.abs(x), Potenzfunktion xⁿ = Math.pow(x,n), Wurzelfunktion √x = Math.sqrt(x), Exponentialfunktion e^x = Math.exp(x), natürlicher Logarithmus ln(x) = Math.log(x), trigonometrische Funktionen sin(x) = Math.sin(x), cos(x) = Math.cos(x), tan(x) = Math.tan(x), trigonometrische Umkehrfunktionen arcsin(x) = Math.asin(x), arccos(x) = Math.acos(x), arctan(x) = Math.atan(x).