Mathematik
> Monte-Carlo-Verfahren

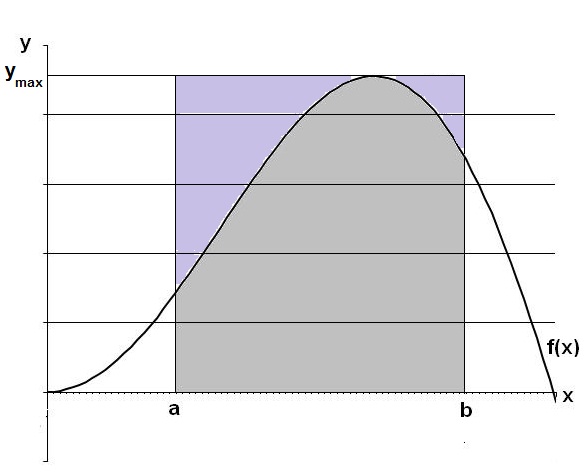
Monte-Carlo-Verfahren zur Bestimmung der Fläche zwischen einer Funktion f(x)≥0 und der x-Achse auf einem Intervall [a; b] -> A = _a∫^b f(x) dx = A_R*n_Treffer/n mit A_R = (b-a)*y_max, y_max = max{f(x)|x∈[a,b]}, n_Treffer = Anzahl der Zufallspunkte P(x|y) zwischen Funktion und x-Achse, n = Anzahl der insgesamt erzeugten Zufallspunkte.

Funktionseingabe (gemäß JavaScript): Variable x, Klammern (), Addition +, Subtraktion -, Multiplikation *, Division /, Betrag |x| = Math.abs(x), Potenzfunktion xⁿ = Math.pow(x,n), Wurzelfunktion √x = Math.sqrt(x), Exponentialfunktion e^x = Math.exp(x), natürlicher Logarithmus ln(x) = Math.log(x), trigonometrische Funktionen sin(x) = Math.sin(x), cos(x) = Math.cos(x), tan(x) = Math.tan(x), trigonometrische Umkehrfunktionen arcsin(x) = Math.asin(x), arccos(x) = Math.acos(x), arctan(x) = Math.atan(x).